BOJ 2612 - 선분 그룹

문제

x1 y1 x2 y2로 표현되는 선분 N 개가 주어진다.

두 선분이 한 점에서라도 만나면 같은 그룹이라 정의할 때,
N 개의 선분이 구성하는 그룹의 개수, 그룹들 중 가장 많은 선분이 속한 그룹의 선분 수를 출력해야 한다.

풀이

점 A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4)로 주어진 두 선분 AB, CD에 대해,

1. AB, CD가 평행하지 않음
   1. 교차점까지 두 선분이 닿지 않음
   2. 교차점까지 두 선분이 닿음 => 같은 그룹
2. AB, CD가 평행
   1. 두 선분이 한 직선에 속함
      1. 만나는 부분이 있음 => 같은 그룹
      2. 만나는 부분이 없음
   2. 두 선분이 만나지 않음

1-1, 2-1-1의 경우만 같은 그룹에 속한다.

1-1

CCW(A, B, C)는 두 벡터 AB(x2-x1, y2-y1, 0), BC(x3-x2, y3-y2, 0)를 외적하는 것이다.

CCW(A, B, C)의 의미

CCW의 목적은 세 점이 주어졌을 때, 기준이 되는 선분으로부터 한 점이 어느 쪽에 위치해있는지 판별하는 것이다.
기준이 되는 선분은 AB, BC, CA 모두 가능하지만, AB를 기준으로 하자.
벡터 AB, BC의 외적을 구했을 때, 0이면 A, B, C가 같은 선상에 있고, 음수나 양수는 어느 한쪽에 있다는 것이다.

따라서 CCW(A, B, C) * CCW(A, B, D)가 음수면 점 C와 D가 선분 AB를 기준으로 서로 반대편에 위치한다.

CCW(A, B, C) * CCW(A, B, D)로 선분 AB에 대한 점 C, D의 상대적인 위치를 알 수 있다. 하지만, 이 사실만으로 선분 AB와 CD가 교차한다고 말할 수는 없다. 아래와 같이 교차점이 선분에 포함되지 않을 수 있기 때문이다.

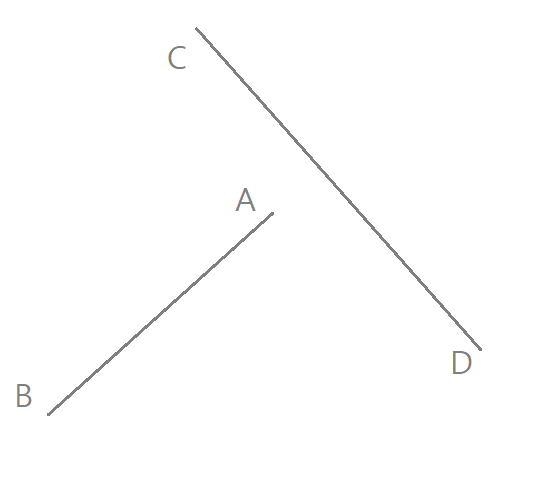
따라서 CCW(A, B, C) * CCW(A, B, D), CCW(C, D, A) * CCW(C, D, B)가 둘 다 음수여야만 선분 AB, CD가 교차한다.

2-1-1

CCW(A, B, C) * CCW(A, B, D)가 0이면 C, D 중 최소 한 점이 선분 AB와 일직선 상에 있는 것이다.
CCW(C, D, A) * CCW(C, D, B)에 대해서도 마찬가지이므로,
CCW(A, B, C) * CCW(A, B, D), CCW(C, D, A) * CCW(C, D, B) 둘 다 0이면 두 선분이 한 직선에 속하는 것이다.

이제 두 선분이 공통으로 가지는 구간이 있는지 확인해야 하는데, 둘 다 y축에 평행하면 x좌표로 비교할 수 없기 때문에 둘 중 한 선분의 두 점의 x좌표가 같은지 확인한다.
같으면 y좌표를 이용해서 두 선분이 공통으로 포함하는 구간이 있는지 확인하고, 아닐 경우 x좌표를 이용해서 확인한다.

선분의 그룹은 disjoint set을 이용해서 구현했다.
가장 큰 그룹의 크기는 N 개의 선분의 그룹을 모두 확인해서 셋다.

소스코드

#include<iostream>
#include<vector>
#include<utility>
#define x first
#define y second
using namespace std;
typedef pair<int, int> pii;
typedef pair<pii, pii> line;
typedef vector<int> vi;

int getp(vi& g, int a) {
	if(g[a]==a) return a;
	return g[a]=getp(g, g[a]);
}

int setp(vi& g, int a, int b) {
	a=getp(g, a);
	b=getp(g, b);
	if(a>b) {
		g[a]=b;
		return b;
	}
	else {
		g[b]=a;
		return a;
	}
}

int chkp(vi& g, int a, int b) {
	return getp(g, a) == getp(g, b);
}

int apart(int a, int b, int c, int d) {
	int min1, min2, max1, max2;
	if(a>b) min1=b,max1=a;
	else min1=a,max1=b;
	if(c>d) min2=d,max2=c;
	else min2=c,max2=d;
	
	return max1<min2 || max2<min1;
}

long long ccw(pii a, pii b, pii c) {
	return a.x*b.y+b.x*c.y+c.x*a.y-(a.y*b.x+b.y*c.x+c.y*a.x);
}

int inter(line a1, line a2) {
	long long c1=ccw(a1.x, a1.y, a2.x)*ccw(a1.x, a1.y, a2.y), c2=ccw(a2.x, a2.y, a1.x)*ccw(a2.x, a2.y, a1.y);
	if(c1>0 || c2>0) return 0;
	if(c1==0 && c2==0) {
		if(a1.x.x==a1.y.x) return !apart(a1.x.y, a1.y.y, a2.x.y, a2.y.y);
		else return !apart(a1.x.x, a1.y.x, a2.x.x, a2.y.x);
	}
	return 1;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n;
	cin>>n;
	vi g(n);
	vector<line> va(n);
	for(int i=0;i<n;i++) {
		g[i]=i;
		cin>>va[i].x.x>>va[i].x.y>>va[i].y.x>>va[i].y.y;
		for(int j=0;j<i;j++) {
			if(inter(va[i], va[j])) {
				if(!chkp(g, i, j)) setp(g, i, j);
			}
		}
	}
	
	int m=0, cnt=0;
	vi dset(n, 0);
	for(int i=0;i<n;i++) dset[getp(g, i)]++;
	for(int i=0;i<n;i++) {
		if(dset[i]) cnt++;
		if(m<dset[i]) m=dset[i];
	}
	cout<<cnt<<'\n'<<m;
	return 0;
}

풀고나서

내 코드처럼 CCW를 풀어서 쓰면 총 11번의 연산이 필요한데, 아래처럼 외적을 전개하기 전의 식을 사용하면 연산의 횟수를 7번으로 줄일 수 있다.
kimhc72님의 코드 참조

long long ccw(pii p0, pii p1, pii p2) {
	long long dx1 = p1.x - p0.x;
    long long dx2 = p2.x - p1.x;
    int dy1 = p1.y - p0.y;
    int dy2 = p2.y - p1.y;
    return dx1 * dy2 - dx2 * dy1;
}